El jueves 17/11/2016 iniciábamos nuestros talleres para investigadores y curiosos con un Workshop dedicado a la geoestadística. Aunque el tema es muy complejo y daría para varias sesiones, la idea principal era explicar ciertos conceptos básicos para permitir al investigador jugar con ellos a través del paquete de R gstat.

Este post es un resumen de todo aquello que vimos en el taller. E intentaré responder a las preguntas que fueron surgiendo durante el mismo.

Variables Regionalizadas:

Este concepto, aunque sencillo, es fundamental para entender un análisis geoestadístico de cualquier índole. Un asistente al taller me preguntó en un momento dado:

¿Cómo puedo analizar mis coordenadas?

En realidad, las coordenadas no las analizas de forma directa porque forman parte de tu variable. Lo único que te proporcionan es una localización. Por ejemplo, supongamos que disponemos del número de árboles presentes en las diferentes manzanas de un barrio de una ciudad cualquiera. Si miramos una manzana en concreto, ésta presenta unas coordenadas espaciales que abarcan toda su extensión en el mapa, y asociado a estas coordenadas tenemos el número de árboles presentes.

El número de árboles es nuestra variable y la localización de esta variable la transforma automáticamente en una variable regionalizada.

La base de datos:

Durante el taller, un par de asistentes me dijeron:

Este ejemplo está bien pero yo quiero aplicarlo a mis datos.

Entiendo que uno quiera conseguir resultados rápido, pero antes de abordar sus propios datos, conviene realizar algún ejemplo sencillo para ir aprendiendo.

En el taller presentamos dos ejemplos (Mina Sunshine y el río Mosa), en ambos casos queremos explorar la distribución espacial de minerales. En el caso del río Mosa de forma horizontal y en el de la Mina Sunshine, de forma vertical.

Mina Sunshine

• La mina Sunshine se encuentra en Idaho (Estados Unidos).
• Se trata de una mina principalmente de plata.
• En la mina se han encontrado trazas de oro.
• Tenemos tres alturas diferentes en la mina con diferentes anchuras y longitudes.
• El principal objetivo del investigador es obtener una mapa de la distribución de oro en los distintos pisos de la mina.

La exploración de los datos es una parte esencial en cualquier análisis que realicemos. Podemos usar desde histogramas a funciones de densidad, correlogramas o sencillos mapas de concentraciones.

library(RCurl)
library(sp)
library(gstat)

#Descargar archivo SunshineMine.csv que puede recuperarse desde la url > https://github.com/DataLabUsal/TallerGeo#
url1 <- getURL('https://raw.githubusercontent.com/DataLabUsal/TallerGeo/master/SunshineMine.csv')
AnData <- read.csv(text = url1)
#Recuerda poner el camino de tu archivo. Si no, a través de RStudio puedes descargarlo desde la pestaña "Import Dataset"#


#Exploración de los datos#
head(AnData) #Encabezado de los datos
summary(AnData) #Resumen de los datos

par(mfrow=c(1,2))
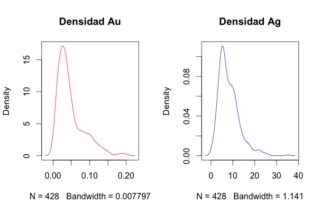
plot(density(AnData$Au),main='Densidad Au',col="red")
plot(density(AnData$Ag),main='Densidad Ag',col="blue")
#Veamos lo que sucede aplicando una transformación logarítmica a nuestros datos
plot(density(log(AnData$Au)),main='Densidad Au',col="red")
plot(density(log(AnData$Ag)),main='Densidad Ag',col="blue")

#Transformamos a SpatialPointsDataFrame (librería 'sp')
coordinates(AnData) <- ~Easting+Elevation

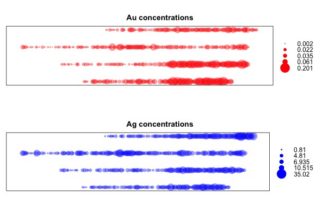
#Gráficos de concentración
b1 <- bubble(AnData, "Au",col="red",alpha=0.4, main = "Au concentrations")
b2 <- bubble(AnData, "Ag",col="blue",alpha=0.4, main = "Ag concentrations")
print(b1, split = c(1, 1, 1, 2), more = TRUE)
print(b2, split = c(1, 2, 1, 2), more = TRUE)
</pre><pre>

Variograma y ajuste

Es una herramienta que permite analizar el comportamiento espacial de una propiedad o variable sobre una zona dada.

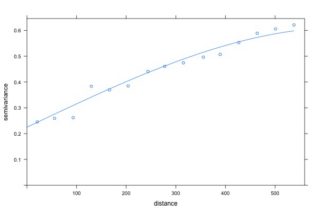
Desde un punto de vista práctico, estudiamos la variación (semivarianza) de nuestra variable en función de las distancias a las que se encuentran nuestras muestras. Podéis encontrar más información al respecto en la presentación que realizamos durante el taller.

Una vez proyectado el variograma experimental, hemos de ajustarlo.

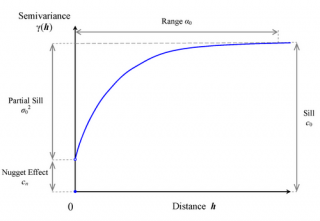
Partes del variograma:

• Nugget : Valor de la semivarianza a distancia cero.
• Sill : Valor al que se estabiliza la semivarianza.
• Rango : Distancia a la que se estabiliza la semivarianza.

Familias de variogramas teóricos:

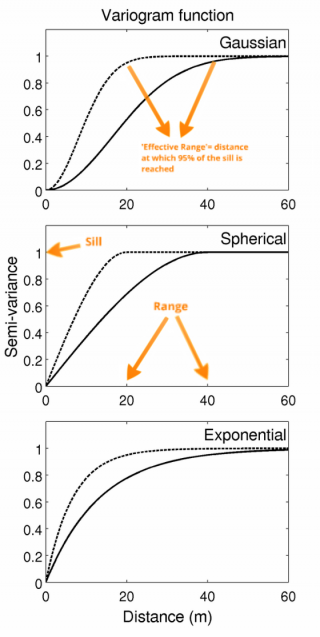
#Variograma#
vg.au <- variogram(log(Au)~1, AnData)
plot(vg.au)
vg.au

#Ajustamos una función a nuestro variograma
vg.au.fit <- fit.variogram(vg.au, model = vgm(1, "Sph", 400, 1))
vg.au.fit

#Visualizamos el ajuste
plot(vg.au,vg.au.fit)

Mallado

Una vez tenemos el modelo ajustado, tenemos que indicar los puntos en el espacio dónde queremos hallar las predicciones de nuestra variable. Es por ello que debemos definir un mallado adecuado en función de nuestras necesidades.

#Mallado específico para nuestros datos (se puede descargar desde la página https://github.com/DataLabUsal/TallerGeo)#
url2 <- getURL('https://raw.githubusercontent.com/DataLabUsal/TallerGeo/master/SunshineMine.grid.csv')
grid <- read.csv(text = url2)
grid_original <- grid
coordinates(grid) <- ~Easting+Elevation

Kriging

Una vez definido el mallado, hemos de hallar los valores de oro. Para ello podemos realizar diferentes análisis.

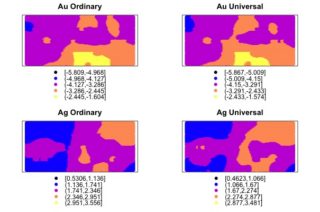
Ordinary Kriging (Kriging básico)

##Ordinary Kriging##
au.krig <- krige(log(Au)~1, AnData, grid, model = vg.au.fit)
names(au.krig)
spplot(au.krig["var1.pred"])

Universal Kriging (Kriging en función de la anchura de nuestras mediciones)

##Universal Kriging##
vg.au.width <- variogram(log(Au)~sqrt(Vein_Width), AnData)
vg.au.width.fit <- fit.variogram(vg.au.width, model = vgm(1, "Sph", 400, 1))
plot(vg.au.width,vg.au.width.fit)
au.krig.width <- krige(log(Au)~sqrt(Vein_Width), AnData, grid, model = vg.au.width.fit)
spplot(au.krig.width["var1.pred"])

 

Cross-Validation

Para poder saber cuál de los dos análisis es más certero. Realizamos un análisis de ambos modelos, basándonos en los datos de los que partíamos.

#Crossvalidation#
cv.ok <- krige.cv(log(Au)~1, AnData, grid, model = vg.au.fit)
summary(cv.ok)
resid.ok <- as.data.frame(cv.ok)$residual
sqrt(mean(resid.ok^2))
mean(resid.ok)
mean(resid.ok^2/as.data.frame(cv.ok)$var1.var)

cv.uk <- krige.cv(log(Au)~sqrt(Vein_Width), AnData, model=vg.au.width.fit)
summary(cv.uk)
resid.uk <- as.data.frame(cv.uk)$residual
sqrt(mean(resid.uk^2))
mean(resid.uk)
mean(resid.uk^2/as.data.frame(cv.uk)$var1.var)

Lo ideal es que nuestros residuales se acerquen a cero y la media de los residuales cuadrados partido su varianza sea próximo a uno. Los resultados, aunque no del todo malos, son mejorables. El taller acabó justo con esta explicación, pero me gustaría continuar un poco más con métodos multivariantes.

Al disponer de la cantidad de plata en los mismos lugares que el oro, podemos aprovechar la correlación espacial de esta variable para predecir la primera. Esta técnica se denomina Cokriging.

Cokriging

El proceso es parecido al que hemos realizado durante el kriging, pero añadiendo la variable plata “Ag”.

##COKRIGING##
#Ordinary Cokriging#
gock <- gstat(NULL, "au", log(Au)~1, AnData)
gock <- gstat(gock, "ag", log(Ag)~1, AnData)
#Se puede realizar un Cokriging Universal de manera parecida a cómo se realizó en el caso del kriging#
#Universal Cokriging#
guck <- gstat(NULL, "au", log(Au)~sqrt(Vein_Width), AnData)
guck <- gstat(guck, "ag", log(Ag)~sqrt(Vein_Width), AnData)

#Variogramas Cruzados#
#Ordinary Cokriging#
cvock <- variogram(gock)
#Universal Cokriging#
cvuck <- variogram(guck)

#Ajuste del modelo inicial#
#Ordinary Cokriging#
gock <- gstat(gock, model = vgm(1, "Sph", 630, 1), fill.all = TRUE)
#Universal Cokriging#
guck <- gstat(guck, model = vgm(1, "Sph", 630, 1), fill.all = TRUE)

#Modelo Lineal de Corregionalización (LMC)
#Ordinary Cokriging#
gock.fit <- fit.lmc(cvock, gock)
plot(cvock, gock.fit)
#Universal Cokriging#
guck.fit <- fit.lmc(cvuck, guck)
plot(cvuck, guck.fit)

#Cokriging#
#Ordinary Cokriging#
cko <- predict(gock.fit, grid)
#Universal Cokriging#
cku <- predict(guck.fit, grid)

El hecho de disponer de una variable correlacionada nos proporciona, en general, mejores resultados que el análisis univariante del kriging. Si queréis profundizar más, echadle un vistazo a nuestra página github.

Víctor Vicente Palacios